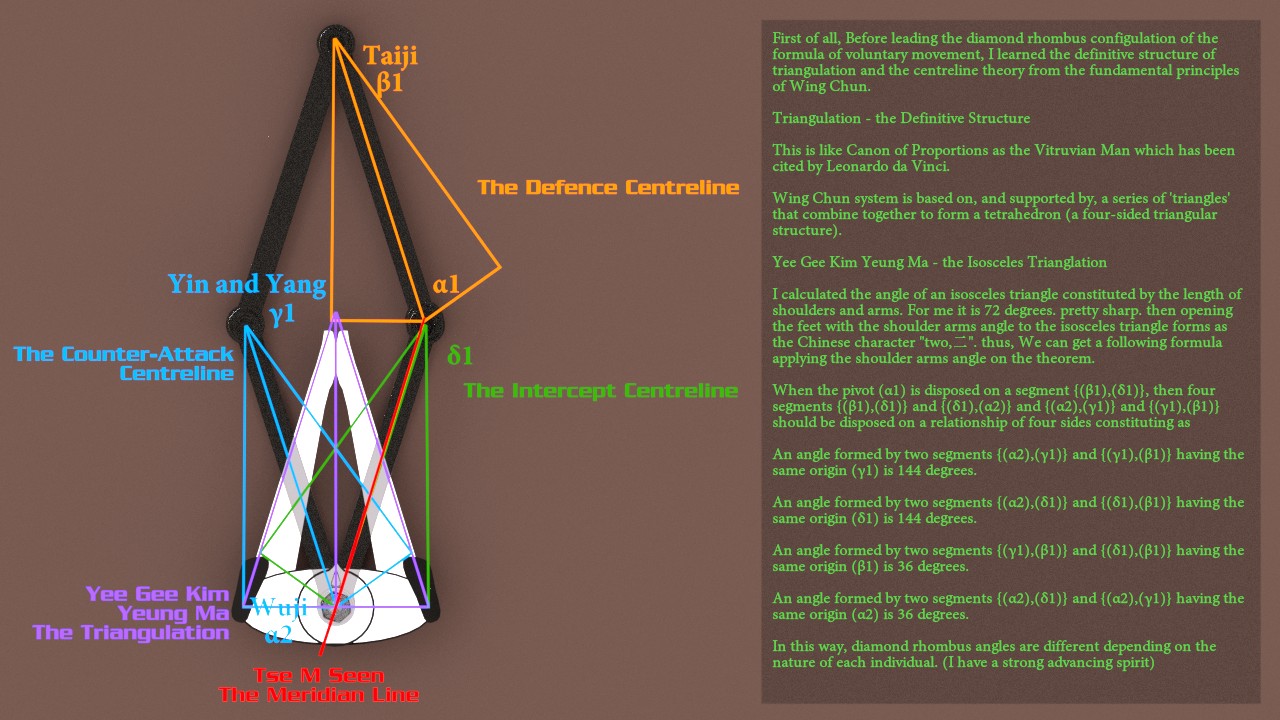
THEOREM

(EN) Now I will explain you about the fundamental theorem of the voluntary movements of animal bodies as well as the invention of the universal biomechanical link mechanism.

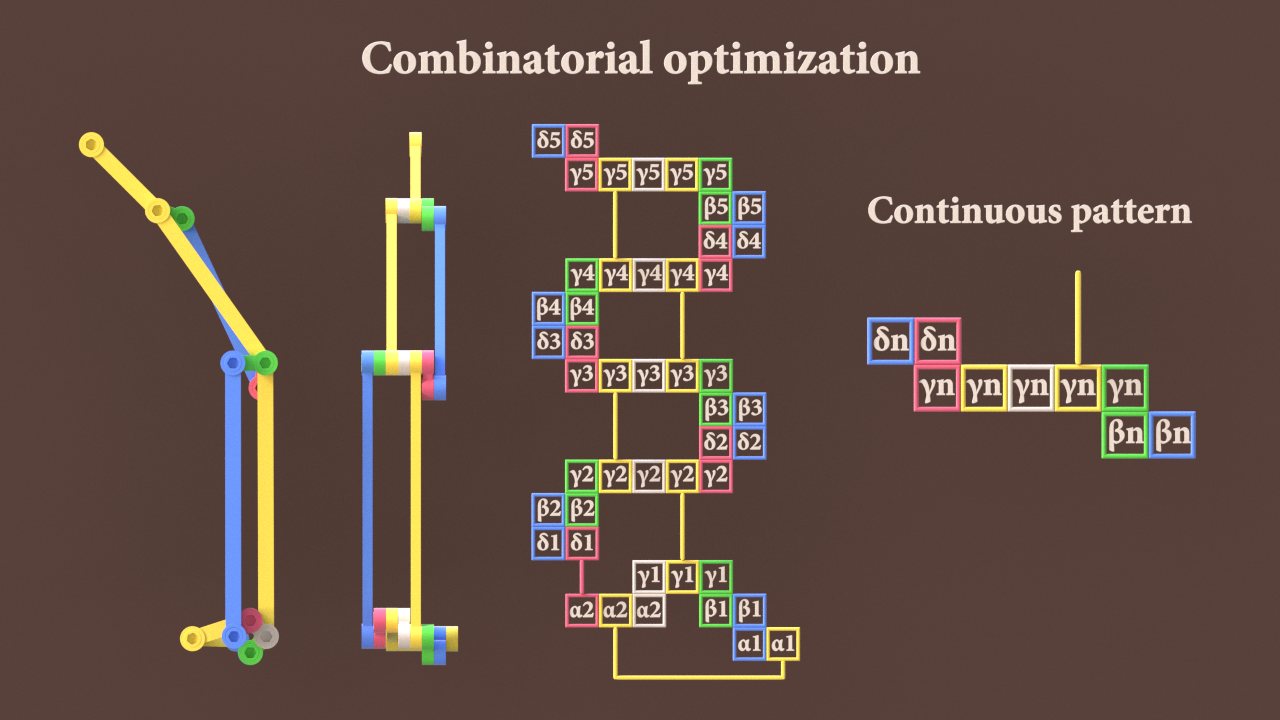
It concerns a link mechanism for expressing natural animal motion has N link elements, each being formed by coupling of a joint (γn) and a joint (βn), the joint (γn) and a joint (δn), and the joint (δn) and a joint (βn+1).

The multiple link elements are coupled together by the joints (γn) and the joints (γn+1). A joint (β1) is coupled to a fulcrum (α1) and is disposed so as to be capable of revolving in an orbit centered on the fulcrum (α1).

A joint (δ1) is coupled to a joint (γ1) via a fulcrum (α2) disposed so as to maintain a constant mutual positional relationship with the fulcrum (α1), or a fulcrum (α2) disposed such that the mutual positional relationship with the fulcrum (α1) can be varied.

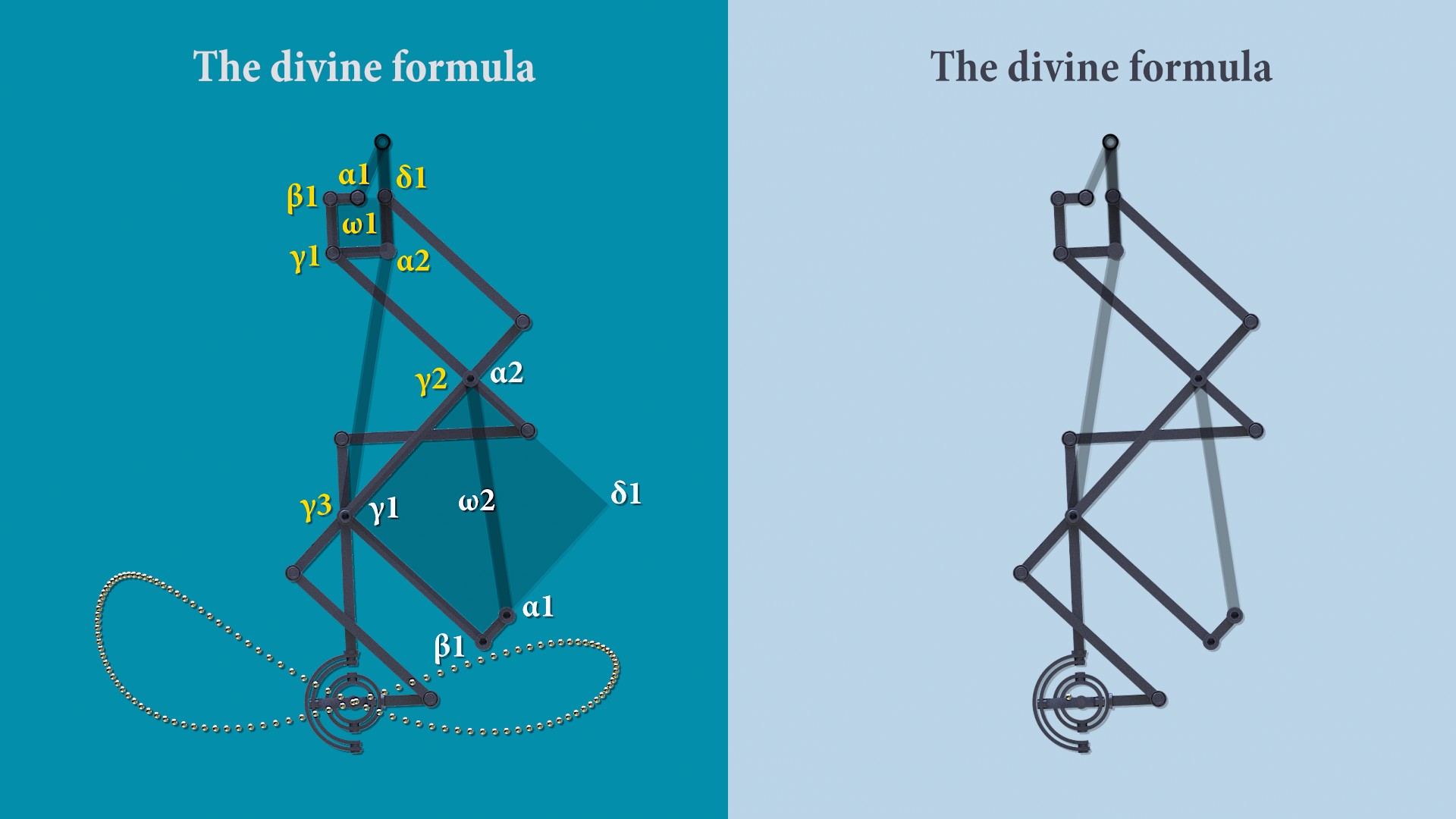
The joint (δ1) and the joint (γ1) are disposed so as to be capable of revolving in an orbit centered on the fulcrum (α2) so as to maintain a constant mutual positional relationship with each other. See the lower figure.

I describe about the optimal condition to meet each volunteer movement cycle based on the above.

An angle formed by two segments [(α2),(γ1)] and [(α2),(δ1)] having the same origin (α2) is immutable.
An angle formed by two segments [(γn),(βn)] and [(γn),(γn+1)] having the same origin (γn) is immutable.
An angle formed by two segments [(γn+1),(γn)] and [(γn+1),(δn+1)] having the same origin (γn+1) is immutable.

When the pivot (α1) is disposed on a segment [(β1),(δ1)], then four segments [(β1),(δ1)] and [(δ1),(α2)] and [(α2),(γ1)] and [(γ1),(β1)] should be disposed on a relationship of four sides constituting as a segment [(β1),(α2)] intersects the center of a segment [(γ1),(δ1)]. and if the segment [(β1),(α2)] is the bisector of an angle formed by two segments [(γ1),(α2)] and [(δ1),(α2)], this articulated mechanism would work best.

Here, the (n) is an integer that is greater than or equal to 1. A segment connecting two joints A and B is denoted [A, B]

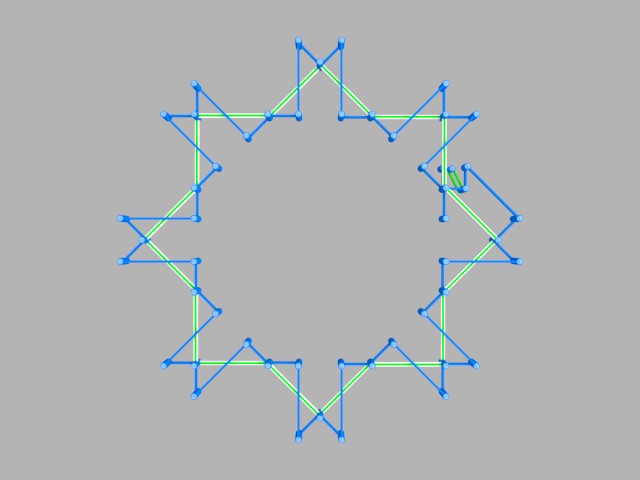
I explain about a mechanical linkage element formed by coupling from the pivot (α1) to the joint (γ5). This is a part of the animal movement as a body, a limbs, a fin of fishes, a wing of insects and birds.

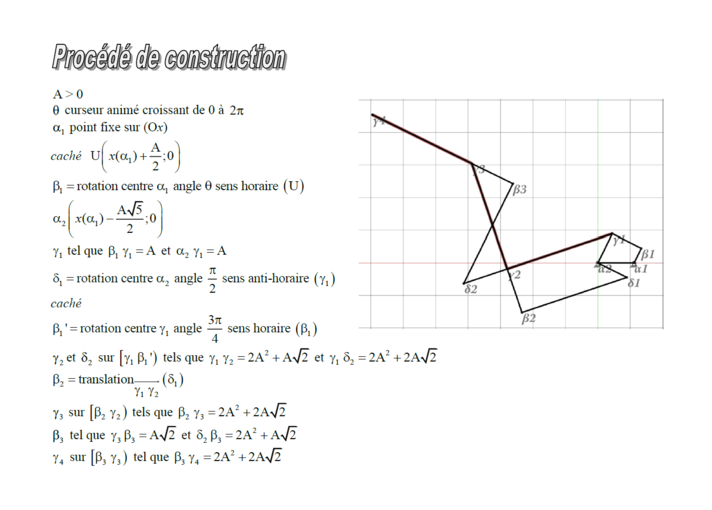
« the lower figure » : The formula was able to get by adjusting the parameters on this theorem.

(FR) Comme une connaissance préalable, je vais vous expliquer d'abord à propos du théorème fondamental des mouvements volontaires des corps d'animaux ainsi que mon invention de mécanisme de liaison biomécanique universelle.

Elle concerne un mécanisme articulé destiné à exprimer un mouvement animal naturel qui présente N éléments d'articulation, chacun étant formé par accouplement d'une articulation (γn) et d'une articulation (βn), de l'articulation (γn) et d'une articulation (δn), et de l'articulation (δn) et d'une articulation (βn+1).

Les éléments d'articulation multiples sont accouplés les uns aux autres au moyen des articulations (γn) et des articulations (γn+1). Une articulation (β1) est accouplée à un pivot (α1) et est disposée de manière à être susceptible de tourner sur une orbite centrée sur le pivot (α1).

Une articulation (δ1) est accouplée à une articulation (γ1) par l'intermédiaire d'un pivot (α2) disposé de manière à maintenir une relation de position mutuelle constante avec le pivot (α1), ou d'un pivot (α2) disposé de sorte que la relation de position mutuelle avec le pivot (α1) puisse être modifiée.

L'articulation (δ1) et l'articulation (γ1) sont disposées de manière à être susceptibles de tourner sur une orbite centrée sur le pivot (α2) de manière à maintenir une relation de position mutuelle constante l'une avec l'autre. Voir « la figure ci-dessous »

Je décris que la condition optimal pour faire répondre chaque cycle de mouvement volontaire basée sur le ci-dessus.

Un angle qui est formé par deux segments [(α2),(γ1)] et [(α2),(δ1)] ayant la même origine (α2) est immuable.
Un angle qui est formé par deux segments [(γn),(βn)] et [(γn),(γn+1)] ayant la même origine (γn) est immuable.
Un angle qui est formé par deux segments [(γn+1),(γn)] et [(γn+1),(δn+1)] ayant la même origine (γn+1) est immuable.

Lorsque le pivot (α1) est disposée sur un segment [(β1),(δ1)], alors quatre segments [(β1),(δ1)] et [(δ1),(α2)] et [(α2),(γ1)] et [(γ1),(β1)] devrait être disposées sur une relation de quatre côtés constituant que un segment [(β1),(α2)] se croise au centre du segment [(γ1),(δ1)]. et si le segment [(β1),(α2)] est la bissectrice d'un angle formé par deux segments [(γ1),(α2)] et [(δ1),(α2)], ce mécanisme articulé fonctionnerait le mieux.

Dans la description, (n) est un nombre entier qui est supérieur ou égal à 1. Un segment reliant deux articulations A et B est noté [A,B]

J'explique sur un élément d'articulation formé par accouplement depuis le pivot (α1) jusqu'à l'articulation (γ5). Il s'agit d'une part du mouvement animal comme un fuselage, un membre, une nageoire des poissons, une aile des insectes et oiseaux.

« la figure ci-dessous » : La formule a été en mesure d'obtenir en ajustant les paramètres de ce théorème.

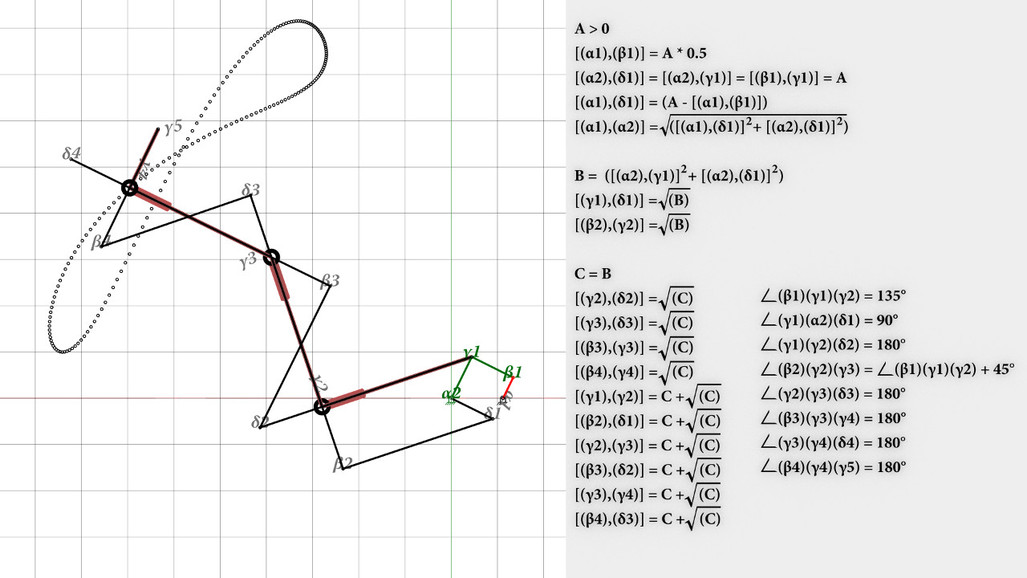
« the lower figure » : An example of combination optimization

« la figure ci-dessous » : Un exemple d'optimisation de combinaison

The formula