Task 7.1 : Serpent crawling

The fins of manta ray, the wings of insects, etc. There is no bones articulations in them. there are some voluntary movements who cannot show his biomechanical kinetic structure. In this case, we can concentrate on the path curve of the tip of movement. in the summer of 2013, I found that the trajectory of the figure eight gives the voluntary movement of the body of snakes. with the same concept, I also understand the mechanism of the fins of manta ray.

In 2005 I was strongly encouraged to study well by watching the promotional videos produced by François Junod, the master of automata produtor, in Sainte-Croix. I made some research about one of his masterpieces, which is the flying carpet (also referred to as a magic carpet) and the Arab caliph (king). It was one of the main pieces of his work. « https://youtu.be/hm9G8Lo8V4Q »

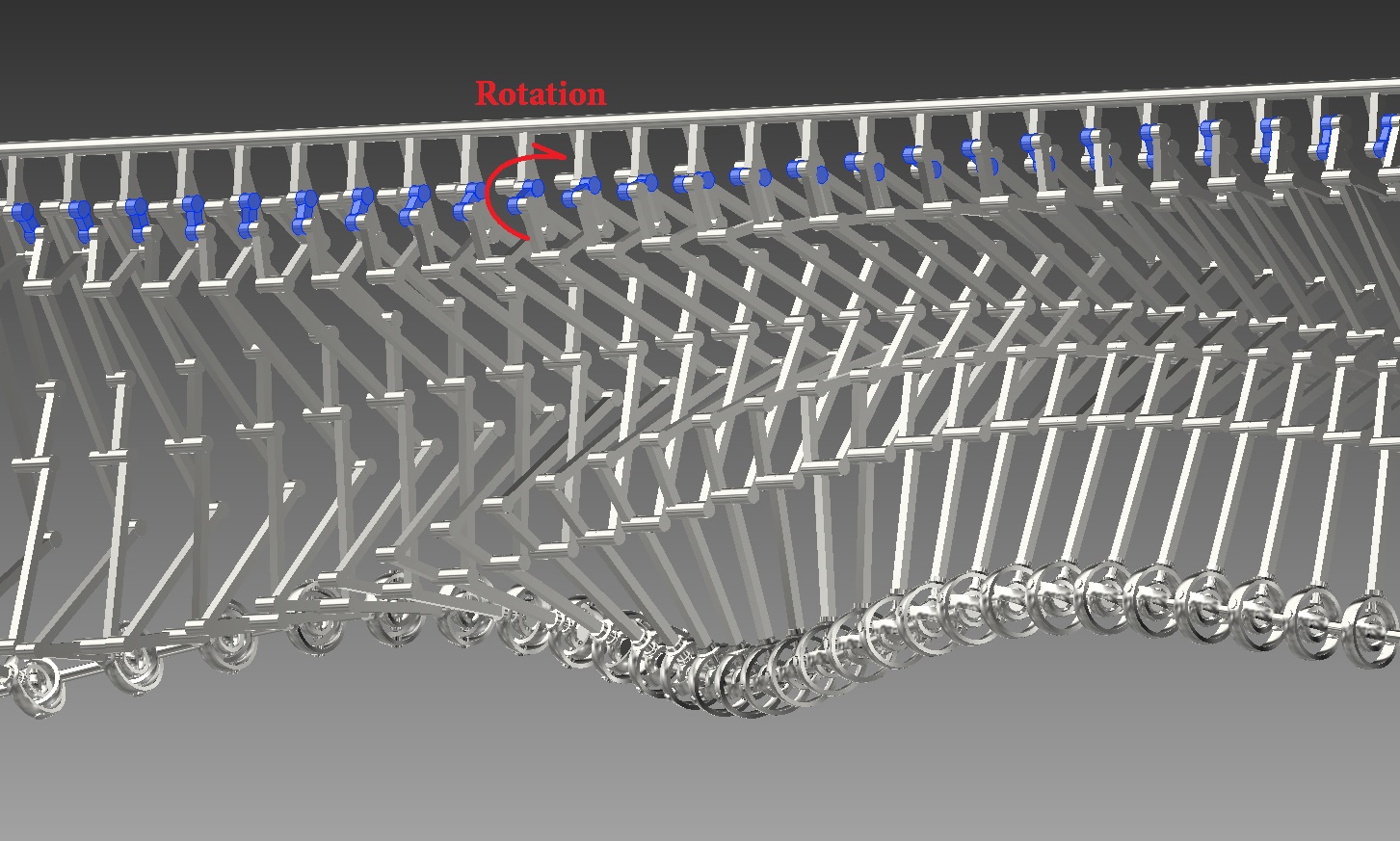
Then, I found a logical order in the sinusoid wave. There are similar kinds of mechanism that are arranged in parallel when their phases shift. ... Then at the cafe of Pompidou center in Paris when I made two shot glasses roll horizontally, I found that to create a crawling snake figure, I could draw a trajectory figure in shape of the number eight, which can also represent infinity. The trajectory of the number eight also appears in Chinese martial arts that imitate the movements of natural animals. Please see below for the details of the trajectory of the formula. « http://goo.gl/bKevoS »

I furthered my research on basic mechanical linkage to draw the trajectory of the figure eight. This mechanical linkage basis, which has fine proportions, can be expressed with geometric shapes, the combination of a square and a parallelogram, two isosceles and orthogonal triangles, and an isosceles right triangle. This trajectory of the figure eight is in flat shape. There is a circle on the left and another on the right, and they are slightly different from each other. One end is pointed and the other end is rounded.

The perceptual functions in animals is not high in accuracy as compared with mechanical devices. Instead, animals have automatic correction functions eliminates unnecessary noise and compensates for missing parts.

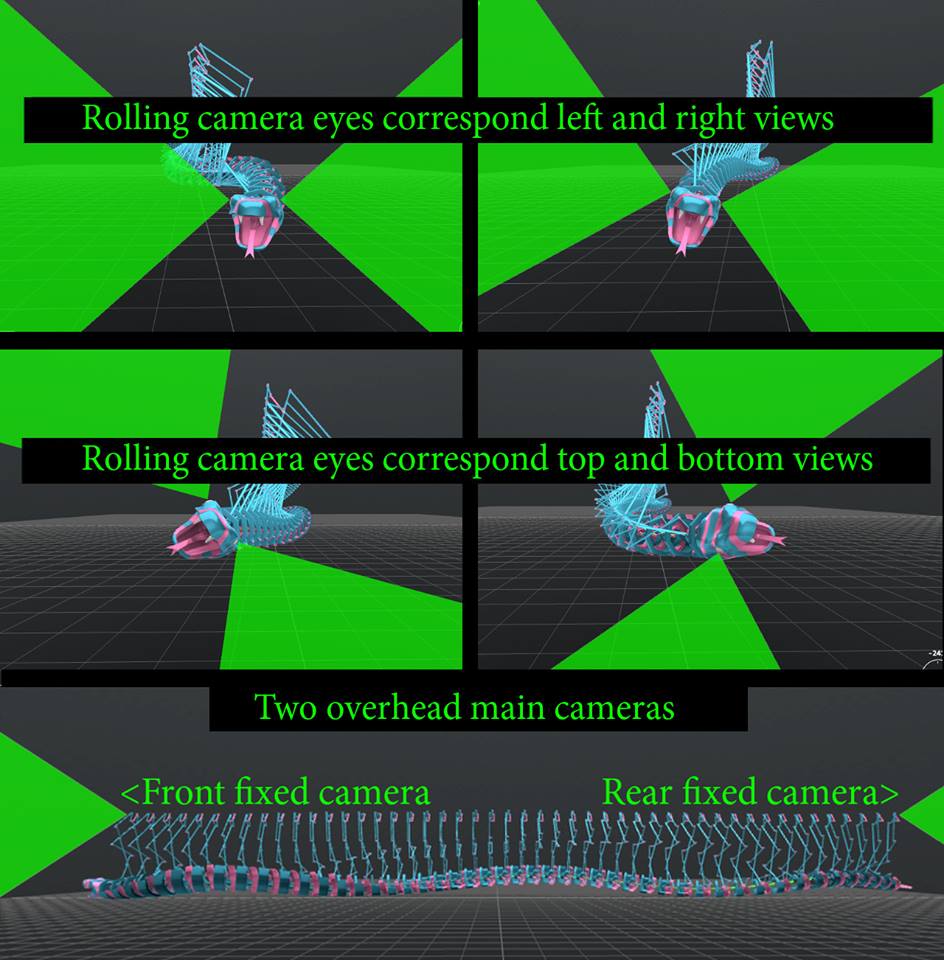
An example of the biomechanical mechanism of a snake-typed drone,

- Perception of own movement vector
There are two visual devices(eyes) in the head, and data is acquired.

- Perception of position information of own self and target
There is a center(the centroid) of the global coordinate system to above of the body. There is a main perception device here and acquires GPS data.

« https://youtu.be/LXBzuwsEwdk , https://youtu.be/L4FcjRzYSHE »

Animal bodies through the process of learning, construct the cognitive structure on the relationship between the target and the way to reach it. Thanks to this cognitive structure or cognitive map, we can grasp the position and condition of target and body, even if the perception accuracy of the body is low.